---

그림과 같이 사각형 $ABCD$가 원 $\omega$에 내접한다고 하고, $AC$, $BD$는 점 $F$에서 만나고, 직선 $BA$와 직선 $CD$가 점 $E$에서 만난다. 점 $F$에서 $AB$, $CD$ 위에 내린 수선의 발을 각각 $G$, $H$라 하고, 점 $M$, $N$은 각각 선분 $BC$, $EF$의 중점이라 하자. 삼각형 $MNG$의 외접원과 선분 $BF$의 유일한 교점을 $P$, 삼각형 $MNH$의 외접원과 선분 $CF$의 유일한 교점을 $Q$라 할때, 직선 $PQ$가 직선 $BC$와 평행함을 보여라.

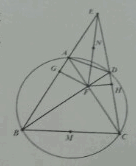
(2013년 3월 13일, 출처, 4시간 30분)

양의 정수 $n$에 대하여 $f(n)$을 \[f(n)=\min_{m\in \mathbb{Z}} \left\lvert \sqrt2-\frac{m}{n}\right\rvert\]로 정의하자. (여기서 $\mathbb{Z}$는 정수 전체의 집합이다.) 단조증가하는 양의 정수의 수열 $\{n_i\}$와 어떤 상수 $C$가 있어서 모든 $i=1,2,3\ldots$에 대해 \[f(n_i)<\frac{C}{n_i^2}\]을 만족시킨다고 하자. 이때 모든 $i=1,2,\ldots$에 대하여 $n_i\ge q^{i-1}$이 되게 하는 실수 $q>1$가 존재함을 증명하라.
(2013년 3월 13일, 출처, 4시간 30분)

$1,2,\ldots ,n$($n \ge 3$)의 번호가 적혀있는 작은 공들이 있다. 아래 서술한 색칠 방법을 써서 각각의 공을 빨강, 노랑, 파랑, 보라 네 가지 중의 하나를 칠한다: 먼저 $n$개의 공을 원 주 위에 임의로 배열한다. 시계방향 순서대로 임의의 연속 3개의 공에 대하여 그 번호가 $i$, $j$, $k$라 하자.
(1) 만일 $i \gt j \gt k$이면 $j$번 공에 빨강을 칠한다.
(2) 만일 $i \lt j \lt k$이면 $j$번 공에 노랑을 칠한다.
(3) 만일 $i \lt j$, $k \lt j$이면 $j$번 공에 파랑을 칠한다.
(4) 만일 $i \gt j$, $k \gt j$이면 $j$번 공에 보라를 칠한다.
$n$개의 공의 두 가지 염색방법이 다르다 함은 적어도 하나의 공이 두 가지 염색방법에서 다른 색을 가진다는 뜻이다. 서로 다른 색칠 방법의 수를 구하여라.
(2013년 3월 13일, 출처, 4시간 30분)

$1$보다 큰 정수 $n$, $k$에 대해 $a_1,a_2,\ldots,a_n,c_1,c_2,\ldots,c_m$을 다음 두 조건을 만족하는 음아닌 실수라 하자.
(1) $a_1\ge a_2\ge \cdots \ge a_n$이고 $a_1+a_2+\cdots+a_n=1$.
(2) 모든 정수 $m\in\{1,2,\ldots,n\}$에 대해 $c_1+c_2+\cdots+c_m\le m^k$.
이때 $c_1a_1^k+c_2a_2^k+\cdots +c_n a_n^k$의 최대값을 구하여라.
(2013년 3월 14일, 출처, 4시간 30분)

삼각형 $ABC$의 변 $BC$, $CA$, $AB$의 중점을 각각 $L$, $M$, $N$이라 하고, 삼각형 $ABC$ 내부에 \[ PL:PM:PN=BC:CA:AB\]가 되는 점 $P$가 있다. 직선 $AP$, $BP$, $CP$가 삼각형 $ABC$의 외접원과 만나는 $A$, $B$, $C$가 아닌 점을 각각 $D$, $E$, $F$라 하자. 이때 삼각형 $APF$, $APE$, $BPF$, $BPD$, $CPD$, $CPE$ 각각의 외심을 모두 지나는 원이 존재함을 증명하라.
(2013년 3월 14일, 출처, 4시간 30분)

아래 조건을 만족하는 집합이 존재할 모든 $1$보다 작은 양의 실수 $r$을 모두 구하여라.
임의의 실수 $t$에 대해 $t$, $t+r$, $t+1$ 중 정확히 하나만 집합 $S$의 원소이며, $t$, $t-r$, $t-1$ 중 정확히 하나만 $S$의 원소이다.
(2013년 3월 14일, 출처, 4시간 30분)

$2$ 이상의 정수 $k$에 대해 $T_k=\{(x,y): x,y=0,1,\ldots,k-1\}$를 평면 위의 $k^2$개의 격자점의 집합이라 하자. 집합 $T_k$에 있는 두 점 사이의 서로 다른 거리의 수열을 $d_1(k)>d_2(k)>\cdots$이라 하자. $T_k$에 있는 두 점 사이의 거리가 정확히 $d_i(k)$인 쌍의 수를 $S_i(k)$라 하자.
임의의 세 양의 정수 $m \gt n\gt i$에 대해 $S_i(m)=S_i(n)$임을 증명하라.
(2013년 3월 18일, 출처, 4시간 30분)

다음 성질을 만족하는 양의 정수의 단조 증가 수열이 존재함을 보여라.
(1) 어떤 수 $K$가 있어서 $a_n\lt 1.01^n K$이 모든 양의 정수 $n$에 대해 성립한다.
(2) 수열 $\{a_n\}$의 유한개의 항을 어떻게 합하여도 완전제곱수가 아니다.
(2013년 3월 18일, 출처, 4시간 30분)

평면 위의 점 $6$개의 집합 $A$에 대해 $n(A)$를 그 점 중 3개 이상을 만나는 반지름 $1$인 원의 수라고 하자. $n(A)$의 최대값을 구하여라.
(2013년 3월 18일, 출처, 4시간 30분)

정수 $N>1$을 소인수분해한 것이 $N=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}$라 할 때 $\Omega(N)=\alpha_1+\alpha_2+\cdots+\alpha_k$라 하자. 양의 정수 $a_1,a_2,\ldots,a_n$에 대해 다항식 $P(x)=(x+a_1)(x+a_2)\cdots (x+a_n)$이 모든 양의 정수 $k$에 대해 $\Omega(P(k))$가 짝수가 된다고 한다. 이때 $n$이 짝수임을 증명하라.
(2013년 3월 19일, 출처, 4시간 30분)

다음 성질을 만족하는 양의 정수 $m$ 중 가장 큰 것을 찾아라.
양의 정수가 모두 정확히 한번씩 나타나는 임의의 양의 정수의 수열 $a_1,a_2,a_3,\ldots$에는 항상 길이가 $m$이고 공차가 홀수인 등차수열을 이루는 부분수열 $a_{i_1}, a_{i_2},\ldots,a_{i_m}$ ($i_1\lt i_2\lt \cdots \lt i_m$)이 존재한다.
(2013년 3월 19일, 출처, 4시간 30분)

$1$보다 큰 양의 정수 $n$과 음 아닌 실수 $a_0,a_1,\ldots,a_n$이 있다. 정수 $k=0,1,\ldots,n$에 대해 $S_k=\sum_{i=1}^k \binom{k}{i} a_i$라 할 때 다음 부등식을 증명하라.
\[ \frac1n \sum_{k=0}^{n-1} S_k^2 -\frac1{n^2}\left( \sum_{k=0}^n S_k\right)^2 \le \frac4{45} (S_n-S_0)^2.\]
(2013년 3월 19일, 출처, 4시간 30분)

최대공약수가 $1$인 $n\ge 2$개의 양의 정수 $a_1$, $a_2,\ldots,a_n$에 대해, 그 합을 $A$라 하고, $A$와 $a_i$의 최대공약수를 $d_i$라 하며, $a_1,a_2,\ldots,a_n$에서 $a_i$를 뺀 나머지 $n-1$개 수의 최대공약수를 $D_i$라 하자. 이때 $\prod_{i=1}^n \frac{A-a_i}{d_i D_i}$의 최솟값을 구하여라.
(2013년 3월 24일, 출처, 4시간 30분)

삼각형 $ABC$의 외접원의 중심이 $O$라 하고, 외접원에서 $B$에서 $A$를 지나 $C$로 가는 원호의 중점을 $P$라 하고 $PQ$가 외접원의 지름이 되게 $Q$를 잡자. 삼각형 $ASBC$의 내심 $I$에 대해 직선 $PI$와 $BC$의 교점을 $D$라 하자. 삼각형 $AID$의 외접원과 직선 $PA$가 점 $F$($F\neq A$)에서 만난다. 선분 $PD$위의 점 $E$가 $DE=DQ$를 만족한다. 삼각형 $ABC$의 외접원의 반지름을 $R$, 내접원의 반지름을 $r$이라 하자. 만일 $\angle AEF=\angle APE$이면 $\sin^2 \angle BAC=\frac{2r}{R}$임을 증명하라.
(2013년 3월 24일, 출처, 4시간 30분)

101명의 사람 각각 1번부터 101번까지 적힌 카드를 가지고 1번부터 101번까지 번호가 적힌 둥글게 배치된 의자에 아무렇게나 앚았다. 어떤 사람이 자기가 가진 카드 중 한 장을 두 명의 옆 사람 중 한 명에게 주는 것을 시행이라 하자. 사람들이 어떻게 앉아있든지 상관없이, $k$번 이하로 시행을 하면 앉은 의자의 번호와 그 사람이 가진 카드의 수가 같도록 할 수 있을 최소의 정수 $k$를 구하여라.
(2013년 3월 24일, 출처, 4시간 30분)

소수 $p$와 양의 정수 $a$, $k$가 $p^a \lt k \lt 2p^a$를 만족한다고 하자. 이때 $n\lt p^{2a}$이고 $\binom{k}{n}$, $n$, $k$를 각각 $p^a$로 나눈 나머지가 모두 같게 하는 양의 정수 $n$이 존재함을 증명하라.
(2013년 3월 25일, 출처, 4시간 30분)

정수 $k\ge 2$와 음 아닌 실수 $a_1,a_2,\ldots,a_n$, $b_1,b_2,\ldots,b_n$에 대해 다음 부등식을 증명하라. \[ \left( \frac{n}{n-1}\right)^{n-1}\left(\frac1n \sum_{i=1}^n a_i^2 \right)+\left(\frac1n \sum_{i=1}^n b_i\right)^2 \ge \prod_{i=1}^n (a_i^2+b_i^2)^{\frac1n}.\]
(2013년 3월 25일, 출처, 4시간 30분)

집합 $P$와 $Q$는 각각 좌표평면 위에 꼭지점이 격자점들로 만들어진 볼록다각형 위나 그 내부에 있는 점의 집합이라 한다. $T=P\cap Q$라 하자. 이때 $T$가 공집합이 아니면서 $T$에 격자점이 없다면 $T$는 어느 내각도 180도가 아닌 볼록사각형임을 증명하라.
(좌표평면 위의 점 $(x,y)$가 격자점이란 $x$, $y$ 모두 정수라는 뜻이다.)
(2013년 3월 25일, 출처, 4시간 30분)