2017년 11월 11일. 4시간 30분. 출처. 장소: 덴마크 Sorø.
loading...
실수의 무한 수열 $a_0, a_1,a_2,\ldots$가 모든 양의 정수 $n$에 대하여 $\frac{a_{n-1}+a_{n+1}}{2}\ge a_n$을 만족시킨다. 이때, 모든 양의 정수 $n$에 대하여 \[ \frac{a_0+a_{n+1}}{2}\ge \frac{a_1+a_2+\cdots+a_n}{n}\]임을 보여라.
실수의 유한 집합 중 그 합은 2이고, 그 제곱의 합은 3이며, 3승의 합은 4, $\ldots$, 9승의 합은 10이 되는 것이 있는가?
(서로 같을 수도 있는) 양의 정수 $x_1$, $\ldots$, $x_m$이 칠판에 적혀있다. 피보나치 수열의 첫 $2018$개 수 $F_1$, $\ldots$, $F_{2018}$ 각각이 칠판에 적혀있는 수이거나 그 수들 여러개의 합으로 나타낼 수 있다고 한다. 이때 가장 작은 $m$은 얼마인가?
(피보나치 수열: $F_1=F_2=1$이며 모든 $k>1$에 대하여 $F_{k+1}=F_k+F_{k-1}$이다.)
$k$개 변수로 구성된 1차 형식이란 어떤 실수 $a_1$, $a_2$, $\ldots$. $a_{k}$에 대하여 $P(x_1,\ldots,x_k)=a_1 x_1+\cdots+a_k x_k$ 꼴로 표현되는 다항식을 뜻한다. 임의의 실수 $x_1$, $x_2$, $\ldots$, $x_{2017}$에 대하여 다음 식이 성립하도록 하는 양의 정수 $n$과 $2017$개 변수로 구성된 1차 형식 $P_1$, $\ldots$, $P_k$가 존재함을 보여라.\[ x_1\cdot x_2\cdot \cdots \cdot x_{2017} = P_1(x_1,\ldots,x_{2017})^{2017}+\cdots+P_n(x_1,\ldots,x_{2017})^{2017}\]
모든 실수 $x$, $y$에 대하여 \[ f(x^2y)=f(xy)+y f(f(x)+y)\]인 함수 $f:\mathbb R\to\mathbb R$를 모두 찾아라.
가로 4칸, 세로 4칸의 판에서 15개 칸을 골라 각 칸에 하나씩의 돌을 놓았다. 돌 두 개가 한 변을 공유하는 이웃한 칸에 있을 때 돌 하나가 다른 돌을 건너뛰어 반대쪽 칸으로 이동하면서 건너뛴 칸에 있던 돌을 없애는 작업을 그 반대쪽 칸이 없는 경우에는 할 수 있다고 한다.
![]() 이때, 어떻게 시작하더라도 마지막에 정확히 돌 하나만 남기도록 하는 것이 가능한가?
이때, 어떻게 시작하더라도 마지막에 정확히 돌 하나만 남기도록 하는 것이 가능한가?
꼭짓점 30개인 완전그래프의 각 변을 빨강 혹은 파랑으로 칠하였다. 같은 색으로 이루어지지 않은 삼각형 하나를 골라서 그 삼각형의 두 변의 색을 바꾸어서 같은 색으로만 이루어진 삼각형이 되도록 하는 작업을 반복하면, 모든 변의 색이 똑같게 할 수 있음을 보여라.
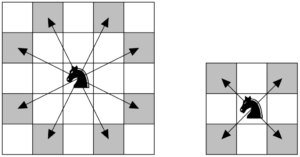
체크의 말 중 기사가 다리를 다쳐서 절뚝거리는 바람에, 원래 규칙과 다르게 정상적인 이동을 한 번 한 다음에는 대각선 방향으로 이웃한 칸으로 이동하는 비정상적인 이동을 한 번 하는 것을 교대로 한다고 하자.
가로 5칸, 세로 6칸인 체스판 위에서 다친 기사가 정상 이동에서 시작하여 움직인다고 할 때, 지났던 칸을 다시 지나지 않고 최대한 많은 칸을 방문하고자 할 때 최대 몇 번이나 이동을 할 수 있는가?
정육각형을 $n$개의 합동인 다각형으로 분할할 수 있으면 그 양의 정수 $n$을 데니시라고 부르자. 이때 $n$과 $2^n+n$이 동시에 데니시가 되는 양의 정수 $n$이 무한히 많음을 보여라.
만득이와 깨비가 벽을 건설하고 있다. 만득이는 녹색으로 된 정육면체 모양의 벽돌을 많이 가지고 있으며 깨비는 빨간색으로 된 같은 크기의 벽돌을 많이 가지고 있다. 땅에 벽돌이 딱 들어갈 크기의 정사각형 $m$개가 분필로 표시되어 있다. 만득이와 깨비는 돌아가면서 분필로 표시된 정사각형 중 하나 위에 골라서 거기에 벽돌을 놓거나, 아니면 이미 놓인 벽돌 위에 벽돌을 놓는 게임을 하는데, 단 각각의 벽돌의 높이는 $n$을 넘을 수 없다. 만득이가 먼저 시작한다.
만득이는 한 행을 모두 녹색을 만들 수 있다는, 즉 같은 높이의 $m$개 벽돌이 모두 녹색이 되게 할 수 있다는데 걸었다. 깨비는 만득이가 그렇게 할 수 없다는데 걸었다. 만득이가 반드시 이길 수 있는 전략이 존재할 양의 정수의 순서쌍 $(m,n)$을 모두 구하여라.
예각삼각형 $ABC$의 수심을 $H$, 내심을 $I$라 하자. 삼각형 $BCI$의 외접원이 선분 $AB$와 점 $P$($\neq B$)에서 만난다. 점 $H$에서 $AI$에 내린 수선의 발을 $K$라 하자. 점 $P$를 점 $K$에 대칭시켜 얻은 점을 $Q$라 하자. 이때, $B$, $H$, $Q$가 한 직선 위에 있음을 보여라.
직선 $\ell$이 원 $S_1$과 점 $X$에서 접하고 원 $S_2$와 점 $Y$에서 접한다. 직선 $\ell$과 평행하고 $S_1$과 $P$에서 만나며 $S_2$와 $Q$에서 만나는 직선 $m$을 그리자. 이때 $XP/YQ$는 $m$을 어떻게 그리던지 일정함을 보여라.
삼각형 $ABC$에서 $\angle ABC=60^\circ$이라고 한다. 삼각형 $ABC$의 내심을 $I$, 외심을 $O$라 하자. 삼각형 $ABC$의 외접원에서 $A$를 지나지 않는 호 $BC$의 중점을 $M$이라 하자. 이때 $MB=OI$이면 각 $\angle BAC$는 얼마인가?
예각 $\angle BAC$ 내부 점 $P$가 $\angle ABP=\angle ACP=90^\circ$을 만족한다. 선분 $BA$와 $CA$ 위에 각각 점 $D$, $E$가 있는데 $BD=BP$이며 $CP=CE$라 한다. 선분 $AC$와 $AB$ 위에 각각 점 $F$, $G$가 있는데 $DF$는 $AB$에 수직이며 $EG$는 $AC$에 수직이라고 한다. 이때 $PF=PG$임을 보여라.
정수 $n\ge 3$에 대하여, 평면 위의 각 변의 길이가 같은 $n$각형에서 내각 중 $180^\circ$보다 크지 않은 것의 수의 최댓값은 얼마인가?
임의의 동아리에서 양의 정수 $N$을 잘 고르고 각 사람에게 적당한 양의 정수를 잘 골라주어서, 임의의 두 사람에 대하여 이 두 사람이 가진 수의 곱이 $N$의 배수일 필요충분조건이 그 두 사람이 친구인 것이 되도록 할 수 있겠는가?
등식 \[x^4+y^3=z!+7\]이 무한히 많은 양의 정수해를 갖는가?
소수 $p>3$에 대하여 $1,2,3,\ldots,\frac{p-1}{2}$의 순열을 $a_1,a_2,\ldots,a_{\frac{p-1}{2}}$라 하자. 소수 $p$가 어떤 값일 때, 아래 정보만 가지고 순열 $a_1,a_2,\ldots,a_{\frac{p-1}2}$를 항상 결정할 수 있는가?
모든 서로 다른 $i,j\in\{1,2,\ldots,\frac{p-1}{2}\}$에 대하여 $a_ia_j$를 $p$로 나눈 나머지
양의 정수 $n$에 대하여 $2017$과 $n\cdot 2017$을 더할때 생기는 받아올림의 횟수를 $a(n)$이라 하자. 예를 들어 $a(1)=1$, $a(2)=1$, $a(3)=0$이다. 이때, \[a(1)+a(2)+\cdots+a(10^{2017}-2)+a(10^{2017}-1)=10\cdot \frac{10^{2017}-1}{9}\]임을 보여라.
부등식 $0<2a<2b<2017$이 성립하며 $a^2+b^2$이 2017의 배수가 되는 양의 정수의 순서쌍 $(a,b)$의 집합을 $S$라 하자. 이때 \[ \sum_{(a,b)\in S} a = \frac12 \sum_{(a,b)\in S} b\]임을 보여라.