(KAIST 수학문제연구회와 xMO 까페의 번역 지원을 받았습니다)

그리스 아테네

한국대표팀: 12위

• 단장: 송용진 (인하대)
• 부단장: 김서령 (서울대), 김명환 (서울대), 오병권 (세종대), 정순영 (서강대), 조용승 (이화여대)
• 대표학생: 김성윤 (서울과고2, 금메달), 박두성 (경기과고1, 은메달), 송용수 (중동고2, 은메달), 이승명 (휘문고3, 금메달), 정영헌 (서울과고1, 동메달), 조세익 (중동고2, 동메달)

---

$AB \neq AC$ 인 삼각형 $ABC$가 있다. $BC$를 지름으로 하는 원이 변 $AB$, $AC$와 각각 점 $M$, $N$에서 만난다. 변 $BC$의 중점을 $O$라 하자. $\angle BAC$의 이등분선과 $\angle MON$의 이등분선이 $R$에서 만난다. 삼각형 $BMR$과 $CNR$의 두 외접원의 한 교점이 변 $BC$ 위에 있음을 증명하여라.

$ab + bc + ca = 0$ 을 만족하는 임의의 실수 $a$, $b$, $c$에 대해 다음을 만족하는 실수 계수의 다항식 $f$를 모두 찾아라. \[ f(a-b) + f(b-c) + f(c-a) = 2 f(a+b+c)\]

아래 그림처럼 6개의 단위 정사각형으로 이루어진 모양, 혹은 이것을 회전하거나 거울대칭시킨 모양을 `갈고리’라 정의하자.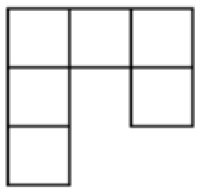여러 개의 갈고리만을 이용해, 겹치거나 밖으로 삐져나오지 않도록 빈 곳 없이 가득 깔 수 있는 $m \times n$ 직사각형들을 모두 구하여라.

$n \geq 3$ 은 정수이고, $t_1, t_2, \dotsc, t_n$ 은 다음을 만족하는 양의 실수들이다.\[ n^2 + 1 > (t_1 + t_2 + \cdots + t_n) \left( \frac1{t_1} + \frac1{t_2} + \cdots + \frac1{t_n} \right)\] $1 \leq i<j<k \leq n$ 인 모든 $i,j,k$에 대해, $t_i$, $t_j$, $t_k$는 삼각형의 세 변의 길이가 될 수 있음을 보여라.

볼록사각형 $ABCD$에서 대각선 $BD$는 $\angle ABC$와 $\angle CDA$ 중 어느 것도 이등분하지 않는다. $ABCD$ 내부의 점 $P$가 다음을 만족한다.\[ \angle PBC = \angle DBA, \qquad \angle PDC = \angle BDA\] $ABCD$가 원에 내접하는 사각형일 때, 또 그 때만, $AP = CP$ 임을 증명하여라.

십진법으로 썼을 때 이웃한 두 자리수의 홀짝이 모두 다른 자연수를 교대수라 부르자. 자신의 배수들 중에 교대수가 있는 자연수들을 모두 구하여라.