2014년 11월 2일.
오전 1-4번 문제 2시간 30분. 오후 5-8번 문제 2시간 30분.
loading...
삼각형 $ABC$의 내심을 $I$라 하고, 직선 $AI$가 변 $BC$와 만나는 점을 $D$라 하자. 삼각형 $ABD$의 내심과 $D$를 지나는 직선이 선분 $BI$와 만나는 점을 $E$, 삼각형 $BCE$의 외접원과 만나는 점을 $P(\ne E)$라 하자. 또, 삼각형 $ACD$의 내심과 $D$를 지나는 직선이 선분 $CI$와 만나는 점을 $F$, 삼각형 $BCF$의 외접원과 만나는 점을 $Q(\ne F)$라 하자. 변 $BC$의 중점이 삼각형 $DPQ$의 외접원 위에 있음을 보여라.
주어진 짝수 개의 양의 실수 $a_1, a_2, \cdots, a_{2n-1}, a_{2n}$에 대하여
\begin{align*}s&=a_1+a_3+a_5+\cdots+a_{2n-1}\\t&=a_2+a_4+a_6+\cdots+a_{2n}\\x_k &= a_k + a_{k+1} + \cdots + a_{k+n-1} \quad (k=1,2,\ldots,2n)\end{align*}이라 하자. 여기서 $a_{2n+1}=a_1$, $a_{2n+2}=a_2$, $\ldots$, $a_{3n-1}=a_{n-1}$이다. 다음 부등식이 성립함을 보여라. \[\frac{s}{x_1} + \frac{t}{x_2} + \frac{s}{x_3}+\frac{t}{x_4}+\cdots +\frac{s}{x_{2n-1}}+ \frac{t}{x_{2n}} > \frac{2n^2}{n+1}\]
꼭짓점 $10$개로 이루어진 아래 그림에서 한 꼭지점으로부터 이웃한 꼭짓점으로 화살표 방향을 따라 움직이는 것을 한 번 이동한 것으로 보자. 꼭짓점 $S$에서 출발하여 총 $n$번 이동하는 방법의 수를 구하여라. 단, 지나갔던 꼭짓점이나 선분을 다시 지나가는 것도 허용한다.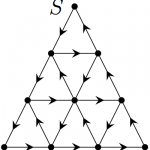
세 양의 정수 $p,q,r$을 모두 나누는 양의 정수가 $1$밖에 없다면, $p$와 $ q+ar$이 서로소가 되도록 하는 정수 $a$가 존재함을 보여라.
양의 정수 $x,y$에 대하여 $x^2y+x$가 $xy^2+7$의 배수가 되는 정수쌍 $(x,y)$를 모두 구하여라.
실수 $p$를 $1+\frac12 +\frac1{2^2}+\frac1{2^3}+\frac{1}{2^4}+ \frac{1}{2^{5}}$라 하자. 등식 \[(x-1)^2 + (y-1)^2 + (z-1)^2 = 27\]을 만족하는 음이 아닌 세 실수 $x,y,z$에 대하여 $x^{p} + y^{p} + z^{p}$의 최댓값을 구하여라.
평행사변형 $ABCD (AB<BC)$가 있다. 삼각형 $ABC$의 내접원이 점 $P$와 $Q$에서 각각 변 $BC$와 $AC$에 접하고, 삼각형 $ACD$의 내접원이 점 $R$에서 변 $CD$에 접한다. 점 $S$는 직선 $PQ$와 $AD$의 교점이고, 점 $T$는 선분 $BC$ 위의 점으로 $AB=BT$를 만족하는 점이며, 점 $U$는 직선 $AR$과 $CS$의 교점일 때 세 직선 $AT$, $BU$, $PQ$가 한 점에서 만남을 보여라.
학생 $n$명과 동아리 $m$개가 있는 어느 중학교에서 아래 조건을 만족하도록 학생들이 동아리에 가입하였다고 한다.
임의의 학생 $x$에 대하여, 동아리들을 적당히 잘 선택하면 그 동아리들에 모두 가입한 회원은 $x$밖에 없다.
각 학생이 가입한 동아리의 수를 $a_1,a_2,\ldots,a_n$이라 할 때, 다음 부등식이 성립함을 보여라.\[a_1!(m-a_1)!+a_2!(m-a_2)!+\cdots+a_n!(m-a_n)!\le m!\]
