2013년 12월 7일 토요일. 오전 3시간 (A1-A6), 오후 3시간 (B1-B6).
loading...
정20면체의 각 면에 음 아닌 정수를 적어서 총 합이 39가 되게 하였다. 이때 적힌 수가 같고 한 꼭지점을 공유하는 두 면이 존재함을 증명하라.
완전제곱수가 아닌 양의 정수의 집합을 $S$라 하자. 집합 $S$의 원소 $n$에 대해 $n\lt a_1\lt a_2\lt \cdots\lt a_r$이면서 $n\cdot a_1\cdot a_2\cdots a_r$이 완전제곱수가 되게 하는 정수의 수열 $a_1,a_2,\ldots,a_r$을 생각했을 때, $f(n)$을 그러한 수열이 가질 수 있는 최소의 $a_r$ 값이라고 하자. 예를 들어 $2\cdot 3\cdot 6$은 완전제곱수이지만 $2\cdot 3$, $2\cdot 4$, $2\cdot 5$, $2\cdot 3\cdot 4$, $2\cdot 3\cdot 5$, $2\cdot 4\cdot 5$, $2\cdot 3\cdot 4\cdot 5$는 완전제곱수가 아니므로, $f(2)=6$이다. 이때 함수 $f$가 일대일함수임을 보여라.
실수 $a_0,a_1,\ldots,a_n$과 $0\lt x\lt 1$인 $x$가 \[ \frac{a_0}{1-x}+\frac{a_1}{1-x^2}+\cdots+\frac{a_n}{1-x^{n+1}}=0\]을 만족시킨다고 한다. 이때 \[a_0+a_1y+\cdots+a_n y^n=0\]이면서 $0\lt y\lt 1$인 실수 $y$가 존재함을 보여라.
원 주변에 유한 개의 숫자 0 또는 1이 적혀있다. 원의 호가 $L$개($L\ge 0$)의 그 중 숫자를 포함하면 그 호의 길이를 $L$이라 하자. 어떤 호 $w$에 대해 $Z(w)$와 $N(w)$를 각각 그 호의 0의 수와 1의 수라고 하자. 임의의 두 호 $w$, $w’$가 길이가 같다면 $\lvert Z(w)-Z(w’)\rvert\le 1$이라 가정하자. 두 수 \[ Z=\frac{1}{k}\sum_{j=1}^k Z(w_j), \quad N=\frac{1}{k}\sum_{j=1}^k N(w_j)\]가 모두 정수가 되게 하는 호 $w_1,w_2,\ldots,w_k$가 존재한다고 하자. 이때 $Z(w)=Z$이고 $N(w)=N$인 호 $w$가 존재함을 증명하라.
정수 $m\ge 3$에 대해 $\binom{m}{3}$개의 실수 $a_{ijk}$ ($1\le i\lt j\lt k\le m$)의 순서쌍이 아래 성질을 만족하면 $\mathbb{R}^n$에 대한 면적양수열이라 부르자:
공간 $\mathbb{R}^n$의 임의의 $m$개의 점 $A_1,A_2,\ldots,A_m$에 대해 \[ \sum_{1\le i\lt j\lt k\le m} a_{ijk} \cdot \operatorname{Area}(\triangle A_i A_jA_k)\ge 0.\] 예를 들어 $a_{123}=a_{124}=a_{134}=1$, $a_{234}=-1$이면 $\mathbb{R}^2$에 대한 면적양수열이다. 이때 $\binom{m}{3}$개의 수가 $\mathbb{R}^2$에 대한 면적양수열이면 $\mathbb{R}^3$에 대한 면적양수열도 됨을 증명하라.
함수 $w:\mathbb Z\times \mathbb Z\to\mathbb Z$를 아래와 같이 정의하자. 정수 $a,b$ ($\lvert a\rvert, \lvert b\rvert \le 2$)에 대해 $w(a,b)$는 아래 표와 같이 정의하고 그 외의 경우에는 $w(a,b)=0$으로 정의한다.
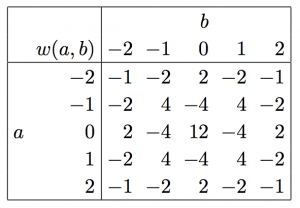집합 $\mathbb Z\times \mathbb Z$의 임의의 유한부분집합 $S$에 대해 \[ A(S)=\sum_{(s,s’)\in S\times S} w(s-s’)\]라 정의하자. 이때 $\mathbb Z\times\mathbb Z$의 임의의 공집합 아닌 유한부분집합 $S$에 대해 $A(S)\gt 0$임을 증명하라. (예를 들어 $S=\{(0,1), (0,2), (2,0), (3,1)\}$이면 $A(S)$의 각 항은 $12, 12, 12, 12, 4,4,0,0,0,0,-1,-1,-2,-2,-4,-4$가 된다.)
양의 정수 $n$에 대해 $c(n)$을 $c(1)=1$, $c(2n)=c(n)$, $c(2n+1)=(-1)^n c(n)$으로 정의하자. 이때 \[ \sum_{n=1}^{2013} c(n)c(n+2)\]의 값을 구하여라.
\[f(x)=1+\sum_{n=1}^N a_n \cos(2\pi nx)\]꼴의 함수 중
(i) 모든 실수 $x$에 대해 $f(x)\ge 0$이고
(ii) 모든 3의 배수 $n$에 대해 $a_n=0$
인 것들을 모은 것의 집합을 $C_N$이라 하고 $C=\cup_{N=1}^\infty C_N$이라 하자. 이때 $f\in C$인 함수 중 $f(0)$ 값의 최대값은 무엇인지 그것의 존재성을 증명하고 값도 구하여라.
집합 $\{1,2,\ldots,n\}$의 공집합 아닌 부분집합의 모음 $P$가 아래 두 조건을 만족한다.
(i) $S,S’\in P$이면 $S\cup S’\in P$이고 $S\cap S’\in P$이다.
(ii) $S\in P$이고 $S\neq \emptyset$이면 $T\in P$이면서 $S$의 원소의 개수보다 하나 적은 개수의 원소를 갖는 $S$의 부분집합 $T$가 존재한다.
함수 $f:P\to \mathbb R$이 $f(\emptyset)=0$이고 모든 $S,S’\in P$에 대해 \[ f(S\cup S’)=f(S)+f(S’)-f(S\cap S’)\]을 만족한다고 하자. 이때 \[ f(S)=\sum_{i=1}^S f_i\]이 모든 집합 $S\in P$에 대해 참이 되게 하는 실수 $f_1,f_2,\ldots,f_n$이 존재하는가?
폐구간 $[0,1]$에서 정의된 연속인 실함수 $f$에 대해 \[ \mu(f)=\int_0^1 f(x)\, dx, \operatorname{Var}(f)=\int_0^1 \left(f(x)-\mu(f)\right)^2\, dx, M(f)=\max_{0\le x\le 1} \lvert f(x)\rvert\]로 정의하자. 이때 폐구간 $[0,1]$에서 정의된 두 연속인 실함수 $f$, $g$에 대해 \[ \operatorname{Var}(fg)\le 2\operatorname{Var}(f) M(g)^2+2\operatorname{Var}(g) M(f)^2\]임을 증명하라.
집합 $X=\{1,2,\ldots,n\}$와 $k\in X$가 주어져있다. 모든 $x\in X$에 대해 $f^{(j)}(x)\le k$가 되는 정수 $j\ge 0$가 존재하는 함수 $f:X\to X$의 수는 정확히 $k\cdot n^{n-1}$임을 증명하라. (여기서 $f^{(j)}$란 함수 $f$를 $j$번 합성한 것이다. 즉 $f^{(0)} (x)=x$이며 $f^{(j+1)}(x)=f(f^{(j)}(x))$이다. )
홀수인 정수 $n\ge 1$이 있다. 철수와 영희가 철수부터 시작해서 교대로 아래와 같은 규칙으로 진행하는 게임을 한다. 게임판은 일렬로 나열한 $n$개의 칸으로 구성되어 있는데 처음에는 모든 칸이 비어있다. 각자 순서가 되면 아래 두 시행 중 하나를 할 수 있다.
- 빈 칸을 하나 골라 돌을 놓는다.
- 어떤 칸에서 돌을 하나 빼고, 그 칸의 왼쪽에 있는 칸들 중 빈 칸이 있다면 그 중 가장 가까운 빈 칸에 돌을 하나 놓고, 마찬가지로 그 칸의 오른쪽에 있는 칸들 중 빈 칸이 있다면 그 중 가장 가까운 빈 칸에 돌을 놓는다.
단, 앞서 나타났던 상황과 똑같은 돌 배치가 되는 상황이 되지 않는 시행만 허용된다고 한다. 철수나 영희 중 시행을 할 수 없는 사람이 진다고 한다. 두 사람 모두 최선을 다한다고 할때, 처음에 철수는 어떤 시행을 해야 하는가?