---

모든 정수 계수 다항식 $p(x)$와 양의 정수 $k$에 대해\[p^{(j)}(k) = \frac{d^j}{dx^j} \left. p(x) \right|_{x=k} \]가 2016의 약수가 될 최소의 양의 정수 $j$를 구하여라.

양의 정수 $m$에 대해, \[\binom{m}{n-1} > \binom{m-1}{n}\]를 만족시키는 가장 큰 정수 $m$을 $M(n)$이라 하자. 이때 \[\lim_{n \to \infty} \frac{M(n)}{n}\] 값을 구하여라.

함수 $f:\mathbb{R}\to\mathbb{R}$가 모든 $x\neq 0$에 대해 \[f(x) + f\left( 1 – \frac{1}{x} \right) = \arctan x\]임을 만족시킨다. (여기서 $y = \arctan x$란 $-\pi/2 < y < \pi/2$이며 $\tan y = x$임을 뜻한다.) 이때 \[\int_0^1 f(x)\,dx\] 값을 구하시오.

양의 정수 $m\ge 4$, $n\ge 4$에 대해 가로 $2m-1$칸, 세로 $2n-1$칸 크기의 직사각형 모양의 영역이 있다. 이 영역을 아래 두 형태의 타일로 덮고자 한다.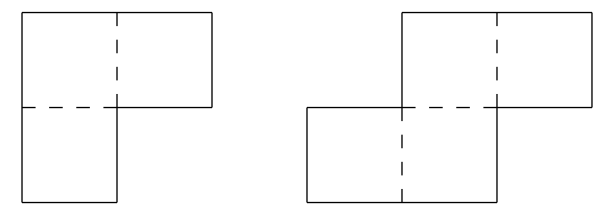

(그림에서 각 타일을 점선을 따라 쪼개면 $1\times 1$ 크기의 정사각형으로 나눠진다.)
각 타일은 각 변이 전체 직사각형의 어떤 변과 평행함을 유지하는 한 회전하거나 대칭시켜 사용할 수 있다. 전체 직사각형 영역을 타일이 겹친 곳 없이 완전히 덮어야 한다.
이때 전체 직사각형 영역을 완전히 덮기 위해 필요한 타일 수의 최솟값은 얼마인가?

두 원소 $g$, $h$에 의해 생성된 유한군 $G$의 차수(order)가 홀수라고 하자. 이때, $G$의 모든 원소는 \[g^{m_1} h^{n_1} g^{m_2} h^{n_2} \cdots g^{m_r} h^{n_r}\]와 같은 꼴로 쓸 수 있음을 보여라. 여기서 $1 \leq r \leq |G|$이며 $m_1, n_1, m_2, n_2, \ldots, m_r, n_r \in \{-1, 1\}$이다. (단, $|G|$는 $G$의 원소의 수)

실수 계수 3차 다항식 $P(x)$가 구간 $[0,1]$에서 해를 가지면 반드시 아래 부등식이 성립하게 할 최소의 상수 $C$ 값을 구하여라.\[\int_0^1 \left| P(x) \right|\,dx \leq C \max_{x \in [0,1]} \left| P(x) \right|.\]

수열 $x_0,x_1,x_2,\dots$이 $x_0=1$이며 모든 for $n \geq 0$에 대해 \[
x_{n+1} = \ln(e^{x_n} – x_n)\]이라 한다. (단, 함수 $\ln$은 자연로그이다.) 이때 무한급수 \[x_0 + x_1 + x_2 + \cdots\]는 수렴함을 증명하고 그 값을 구하여라.

어떤 수 양의 정수 $n$이 완전제곱수이거나 가장 가까운 완전제곱수와의 차이가 완전제곱수라면 그 수 $n$을 ‘대략제곱수’라 부르자. 예를 들어 2016은 대략제곱수인데, 왜냐하면 2016에 가장 가까운 완전제곱수는 $45^2 = 2025$이며 $2025-2016=9$는 완전제곱수이기 때문이다. (물론 1부터 10까지 양의 정수 중에는 6과 7만이 대략제곱수가 아니다.)
양의 정수 $N$에 대해 1 이상 $N$ 이하인 대략제곱수의 수를 $s(N)$이라 하자. 이때 \[
\lim_{N \to \infty} \frac{S(N)}{N^\alpha} = \beta\]인 양의 상수 $\alpha$, $\beta$가 존재함을 보이거나, 그런 상수가 존재하지 않음을 보여라.

평면 위의 유한개의 점의 집합 $S$에서 임의로 세 점을 골라 만드는 삼각형의 넓이가 $1$ 이하라고 하자. 이때, 모든 $S$에 속한 점을 완전히 포함하는 넓이가 $4$인 내부가 채워진 삼각형이 존재함을 보여라.

각 항이 서로 독립적으로 1/2의 확률로 0 또는 1인 $2n \times 2n$ 행렬 $A$가 있다. 이때, $\det(A-A^t)$의 기대값을 $n$에 관한 함수로 구하여라. 단, $A^t$는 $A$의 전치행렬(transpose)을 뜻한다.

다음 조건을 만족하는 모든 함수 $f(1, \infty)\to(1, \infty)$를 찾아라.

모든 $x,y \in (1, \infty)$에 대해 $x^2 \leq y \leq x^3$이면 $(f(x))^2 \leq f(y) \leq (f(x))^3$이다.

다음 값을 구하시오.\[\sum_{k=1}^\infty \frac{(-1)^{k-1}}{k} \sum_{n=0}^\infty \frac{1}{k2^n + 1}\]