2018년 11월 11일. 오전 4문제, 오후 4문제. 제한시간 각각 3시간.
loading...
이차함수 $f(x)$가 다음 조건을 만족할 때, $\displaystyle \frac{ f(8)-f(2)}{f(2)-f(1)}$의 값을 구하여라.
서로 다른 두 실수 $a$, $b$에 대하여 $f(a)=f(b)$이면 $f(a^2 – 6b – 1)= f(b^2 + 8)$이다.
약수의 개수가 $4$ 이상인 양의 정수 $N$에 대하여, $N$의 약수 중 가장 작은 네 개를 각각 제곱하여 더한 값이 $N$과 같아지는 $N$을 모두 구하여라.
이등변삼각형이 아닌 삼각형 $ABC$의 변 $BC$의 중점을 $M$이라 하고, 변 $BC$의 수직이등분선이 삼각형 $ABC$의 외접원과 만나는 점을 $P$라 하자. 이때 $A$와 $P$는 변 $BC$에 대하여 같은 쪽에 있다. 삼각형 $ABM$과 $AMC$의 내심을 각각 $I$, $J$ 라 하고, $\angle BAC = \alpha$, $\angle ABC = \beta$, $\angle BCA = \gamma$라 할 때, $\angle IPJ$를 구하여라.
양의 정수 $n$에 대하여, $x+2y+2z+3w=n$을 만족하는 음이 아닌 정수의 순서쌍 $(x,y,z,w)$의 개수를 $p(n)$이라 하고, 다음 세 조건을 모두 만족하는 음이 아닌 정수의 순서쌍 $(a,b,c,d)$의 개수를 $q(n)$이라 하자.
(i) $a+b+c+d=n$
(ii) $a \ge b \ge d$
(iii) $a \ge c \ge d$
모든 $n$에 대하여 $p(n)=q(n)$임을 보여라.
이등변삼각형이 아닌 예각삼각형 $ABC$의 외심 $O$를 직선 $AB$, $AC$에 대하여 선대칭한 점을 각각 $D$, $E$라 하자. 삼각형 $ADE$의 외접원이 직선 $AB$, 직선 $AC$, 삼각형 $ABC$의 외접원과 만나는 점 중 $A$가 아닌 점을 각각 $K$, $L$, $M$이라 하자. 세 직선 $BC$, $KL$, $AM$이 한 점에서 만남을 보여라.
아래 그림과 같이 $9$개의 작은 원판 $A, B, \ldots, I$와 $11$개의 선분으로 이루어진 도형이 있다. 모든 원판에 실수를 하나씩 쓰고, 각 선분에는 선분의 양 끝 원판에 적힌 두 실수의 차의 제곱을 적는다. 원판 $A$에는 $0$, 원판 $I$에는 $1$을 쓰자. 이때 모든 선분에 적힌 수의 합이 될 수 있는 값 중 가장 작은 것을 구하여라.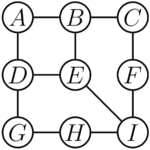
등식 $7^m=5^n+24$를 만족하는 정수의 순서쌍 $(m,n)$을 모두 구하여라.
서로 다른 $n$개의 정수로 이루어진 집합 $S$에 대하여, 다음 두 조건을 모두 만족하는 함수 $f \colon \{1, 2, \ldots, n\} \to S$가 항상 존재함을 보여라. (단, $n$은 $3$ 이상인 정수이다.)
(i) 집합 $\{ f(1), f(2), \ldots, f(n) \}$는 $S$와 같다.
ii) 모든 $1\le i < j < k \le n$에 대하여, $2 f(j) \ne f(i)+f(k)$이다.
