2018년 9월 6일.

5문제, 4시간 30분, 각 문제당 8점.

초급: 중1, 중2. 중급: 중3, 고1. 고급: 고2, 고3.

---

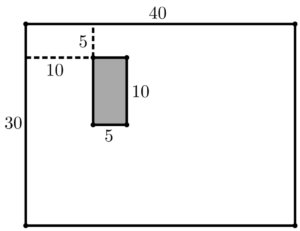
아래 그림과 같이 40×30 종이가 있고 그 안에 검은색으로 색칠된 10×5 직사각형이 놓여져 있다. 우리는 색칠된 직사각형을 정확히 네 번의 가위질로 잘라내고자 한다. 각 가위질은 직선모양으로 이루어지며 자르는 종이를 두 조각으로 나누어야 한다. 가위질을 하여 생긴 두 조각의 종이 중 색칠된 직사각형을 포함한 조각만을 남겨 다음 가위질을 진행한다. 우리의 목표는 색칠된 직사각형을 잘라낼 때까지 가위질을 하는 총 길이를 가장 작게 하는 것이다. 이 목표를 어떻게 달성할 수 있으며, 그 최소한의 길이는 얼마인가? 올바른 커트 방법을 설명하고 최종 답만 적으면 되고, 답을 증명할 필요는 없다.

볼록육각형 $A_1A_2A_3A_4A_5A_6$이 볼록육각형 $B_1B_2B_3B_4B_5B_6$의 내부에 놓여 있고, $A_1A_2 \parallel B_1B_2$, $A_2A_3 \parallel B_2B_3$, …, $A_6A_1\parallel B_6B_1$이라 하자. 이때 단순 육각형 $A_1B_2A_3B_4A_5B_6$과 $B_1A_2B_3A_4B_5A_6$의 넓이가 같음을 보여라. (단순 육각형이란 그것의 어느 두 변도 서로 교차하지 않는 육각형이다.)

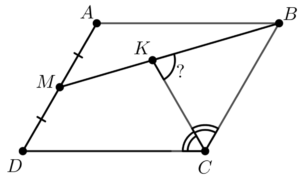평행사변형 ABCD에 대하여, $\angle D = 60^\circ$, $AD = 2$, $AB=\sqrt 3+1$이다. 점 $M$은 $AD$의 중점이고, 선분 $MB$ 위의 점 $K$에 대해 선분 $CK$가 각 $C$의 각이등분선일 때, $\angle CKB$의 값을 구하여라.

원 $\omega$의 내부에 이 원에 접하는 두 원이 있고, 이 두 원의 중심을 $O_1$, $O_2$라 하자. 원$\omega$의 현 $AB$가 이 두 원에 접하고, 두 원은 이 현에 대해 서로 반대쪽에 놓여 있다. $\angle O_1AO_2+\angle O_1BO_2\ge 90^\circ$가 성립함을 보여라.

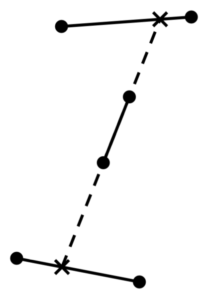
평면위에 (끝점조차도) 서로 겹치지 않게 여러 개의 선분이 놓여 있다. 우리는 아래 그림과 같이 선분 AB의 연장선이 선분 CD와 C와 D 사이에서 만날 때, 선분 AB가 선분 CD를 자른다고 한다.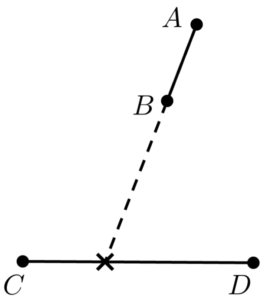

(a) 각선분에 대해 그 선분을 양쪽 방향으로 연장할 때마다 양쪽 연장선 모두 정학히 하나씩의 선분을 자르는 것이 가능한가?

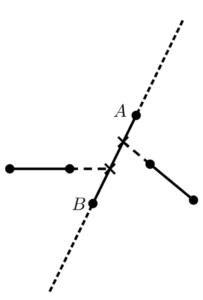(b) 한 선분이 만일 그 선분의 연장선에 의해 생기는 두 개의 면에 대해, 각 면에서 정확히 하나씩 모두 두 개의 선분에 의해 잘린다면, 우리는 그 선분을 둘러싸인다고 한다. (오른쪽 그림의 선분 AB는 둘러싸인 선분의 예이다.) 모든 선분이 둘러싸이는 것이 가능한가?

 

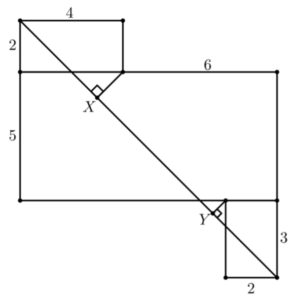
다음 그림과 같이 세 개의 직사각형이 있다. 몇 개 선분의 길이는 주어져 있다. 선분 $XY$의 길이를  구하여라.

볼록사각형 $ABCD$의 두 대각선 $AC$와 $BD$의 교점을 $P$라 하자. $\angle DAC = 90^\circ$이고, $2\angle ADB = \angle ACB$라 한다. $\angle DBC + 2\angle ADC = 180^\circ$일 때, $2AP = BP$ 이 성립함을 보여라.

 두 원 $\omega_1$, $\omega_2$의 중심을 각각 $O_1$과 $O_2$라 하고, 이 두 원이 두 점 $A$와 $B$에서 만난다 하자. 직선 $O_1B$와 $\omega_2$의 두번째 교점을 $C$라 하고, 직선 $O_2A$와 $\omega_1$의 두번째 교점을 $D$라 하자. $X$를 $AC$와 $\omega_1$의 두번째 교점이라 하고, $Y$를 $BD$와 $\omega_2$의 두번째 교점이라 할 때, $CX = DY$가 성립함을 보여라.

각 면이 삼각형인 다면체가 있다. $P$는 이 다면체의 한 변에 있는 임의의 점으로 그 변의 중점이나  양끝점이 아니다. 먼저 $P_0 =P$라 하자. 이후 각 단계에서 $P_i$를 그것을 포함하는 두 면 중 한 면의 무게중심과 직선으로 연결하고, 이 직선이 그 면을 둘러싼 경계와 점 $P_{i+1}$에서 만난다. 이 과정을 다시 $P_{i+1}$과 그 점을 포함하는 면에 대해 진행한다. 이러한 과정을 계속 진행할 때, 모든 면을 모두 통과하는 것은 불가능함을 보여라. (단, 삼각형의 무게중심이란 각 꼭짓점에서 마주 보는 변의 중점을 이은 선분들의 교점이다.)

평행사변형 $ABCD$에 대하여 $\angle DAC = 90^\circ$이다. $A$에서 $DC$에 내린 수선의 발을 $H$라 하자. $P$는 직선 $AC$ 위의 점이고, 직선 $PD$가 삼각형 $ABD$의 외접원에 접한다. 이때, $\angle PBA = \angle DBH$가 성립함을 보여라.

두원 $\omega_1$, $\omega_2$가 서로 다른 두 점 $A$, $B$에서 만난다. 두점 $P\in \omega_1$와 $Q\in \omega_2$에 대하여 $PQ$는 이 두 원의 공통접선이다. $X$가 $\omega_1$ 상의 임의의 점일때, 직선 $AX$와 $\omega_2$가 만나는 점을 $Y$($Y\neq A$)라 하자. $\omega_2$ 상의 점 $Y’\neq Y$에 대하여 $QY =QY’$이다. 직선 $Y’B$와 $\omega_1$의교점을 $X′$($X′\neq B$)이라 할때, $PX=PX’$이 성립함을 보여라. 단,$Y’\neq B$이다.

예각삼각형 $ABC$에 대하여 $\angle A = 45^\circ$이다. 두 점 $O$, $H$를 각각 삼각형 $ABC$의 외심과 수심이라고 하자. $B$에서 $CA$에 내린 수선의 발을 $D$라 하자. 삼각형 $ADH$의 외접원 위에서 $D$를 포함하는 원호 $AH$의 중점을 $X$라 할 때, $DX = DO$가 성립함을 보여라.

다음 조건을 만족하는 모든 정수 $n\gt 3$을 구하여라:

(조건) 각 대각선이 다른 대각선 중 적어도 하나의 수직이등분선이 되는 볼록$n$각형이 존재한다.

사각형 $ABCD$가 한 원에 외접하고, 대각선 $AC$와 $BD$는 서로 수직이 아니다. 이 두 대각선이  교차하여 만들어지는 두 각의 이등분선들이 변 $AB$, $BC$, $CD$, $DA$와 만나는 점을 각각 $K$, $L$, $M$, $N$이라 하자. $KLMN$이 한 원에 내접한다면, $ABCD$도 한 원에 내접함을 보여라.

원에 내접하는 사각형 $ABCD$에 대하여, $A$, $B$를 지나는 원이 변 $CD$와 점 $E$에서 접한다. $C$, $D$를 지나는 또 다른 원이 $AB$와 점 $F$에서 접한다. 점 $G$를 $AE$와 $DF$의 교점, 점 $H$를 $BE$와 $CF$의 교점이라 할 때, 삼각형 $AGF$, $BHF$, $CHE$, $DGE$의 내심들이 한 원 위에 있음을 보여라.